
The length will be 0 for an empty linked list. So, the length of a linked list with ‘head’ as a pointer to 1 st node can be written as: length(head) = 1 + length(head->next) Finding the length of the remaining list can be seen as the same problem and hence can be solved by calling the same function for the next node. So, now we need to find the length of the linked list following the current node and add 1 to it. To solve this problem recursively, we need to break this problem down into subproblems as we do in all recursive approaches.įor a given node of a linked list, we know it will contribute 1 to the total length. Approach (Recursive) to find length of linked list Here, ‘n’ is the number of nodes in the linked list. Space complexity: O(1), as we aren’t using any extra space. Time complexity: O(n), since we are traversing the linked list once. Printf("count of nodes is %d", getCount(head)) * Driver program to test count function*/ Struct Node* current = head // Initialize current * move the head to point to the new node */ (struct Node*) malloc(sizeof(struct Node)) Void push(struct Node** head_ref, int new_data) Of a list and an int, push a new node on the front * Given a reference (pointer to pointer) to the head

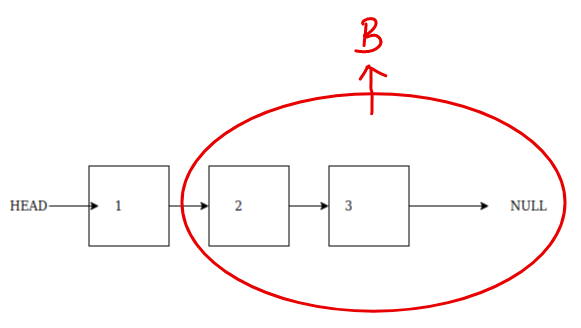
We can keep track of the count of each node visited and that will be the length of the linked list. In an iteration, we visit each node exactly once.
Recursive linked list stack how to#
We know how to iterate through the linked list. Approach (Iterative) to find length of linked list The length of a linked list is the total number of nodes in it. How do we define the length of a linked list? Given a singly linked list, find its length. So let’s just see how to find length of linked list. Therefore, we will discuss how to find length of linked list and one should be aware of how many elements are present in the linked list to perform any kind of operation. We are already aware about how a linked list stores elements in a non-contiguous manner and still connects all the elements via links.


 0 kommentar(er)
0 kommentar(er)
